Cardinal point (optics)

In Gaussian optics, the cardinal points consist of three pairs of points located on the optical axis of an ideal, rotationally symmetric, focal, optical system. For ideal systems, the basic imaging properties (e.g., image size, location, and orientation) are completely determined by the locations of the cardinal points; in fact only four points are necessary: the focal points and either the principal or nodal points. However, the only ideal system that has been achieved in practice is the plane mirror.[1] Consequently, the practical utility of cardinal points would be very limited. However, the cardinal points are widely used to approximate the behavior of real rotationally symmetric, focal, systems.

The three pairs of cardinal points are:

Contents

Modeling optical systems as mathematical transformations

In geometrical optics for each ray entering an optical system a single, unique, ray exits. In mathematical terms, the optical system simply performs a transformation mapping any object ray to an image ray. The object ray and its associated image ray are called conjugates; one can say that the image ray is conjugate to its corresponding object ray or vice versa. This term also applies to corresponding pairs of object and image points and planes.

Optical spaces

Optical spaces facilitate the modeling of optical systems as mathematical transformations. An optical space is a mathematical coordinate system such as a Cartesian coordinate system associated with a refractive index. The analysis of optical systems is greatly simplified by the use of optical spaces which enable designers to place the origin of a coordinate system at any of several convenient locations. In the design of optical systems two optical spaces, object space and image space, are always employed. Additional intermediate spaces are often used as well.

Optical spaces extend to infinity in all directions. The object space does not exist only on the "input" side of the system, nor the image space only on the "output" side. All optical spaces thus overlap completely. Typically, the origin and at least some of the coordinate axes of each space are different. It may not be possible to discern from an illustration to which space a point, ray, or plane belongs unless some convention is adopted. A common convention uses capital letters to label points and lower case letters to indicate distances. Unprimed letters indicate object space and primed letters image space. Intermediate spaces are indicated by additional primes. The same letter is used to indicate a conjugate relationship either between points or distances. The only exception is the use of F and F' to indicate respectively object and image space focal points (which are not conjugate). The term "object point" does not necessarily refer to a point on a specific object but rather to a point in object space; similarly for "image point".

One may wonder how an object point can exist on the "output" side of an optical system or conversely how an image point could be located on the "input" side of an optical system. The answer in both cases is that the points are virtual. Optical spaces are divided into real and virtual parts. Thus, an object point on the "output" side of the system is in the virtual part of object space and is referred to as a virtual object point. Object points on the "input" side are in the real part of object space and are real object points. The situation is reversed for image points.

It is common practice to designate the horizontal axis of an optical space as the z-axis with the positive direction left to right. Similarly, the y-axis is vertical with the positive direction upward.

Rotationally symmetric optical systems; Optical axis, axial points, and meridional planes

An optical system is rotationally symmetric if its imaging properties are unchanged by any rotation about some axis. Occasionally, an optical system is folded using plane mirrors. An optical system is considered rotationally symmetric if it possesses rotational symmetry when unfolded. The (unique) axis of rotational symmetry is the optical axis, or simply "the axis". Any point on the axis (in any space) is an axial point.

Rotational symmetry greatly simplifies the analysis of optical systems, which otherwise must be analyzed in three dimensions. Rotational symmetry allows the system to be analyzed by considering only rays confined to a single transverse plane containing the optical axis. Such a plane is called a meridional plane; it is a cross-section through the system.

It is common practice to place the horizontal axes of both object and image space on the optical axis, so the z-axis, z'-axis and optical axis all overlap. However, in general the origins of object and image space do not conincide but are located at different positions along the optical axis. Likewise, the y and y' axes of object and image space do not overlap.

Ideal, rotationally symmetric, optical imaging system

An ideal, rotationally symmetric, optical imaging system must meet three criteria:

  1. All rays "originating" from any object point converge to a single image point (Imaging is stigmatic).
  2. Object planes perpendicular to the optical axis are conjugate to image planes perpendicular to the axis.
  3. The image of an object confined to a plane normal to the axis is geometrically similar to the object.

In some optical systems imaging is stigmatic for one or perhaps a few object points, but to be an ideal system imaging must be stigmatic for every object point. The word originating is in quotes because in geometrical optics the term ray is not used in quite the same way as mathematicians typically use the term in geometry. In mathematics a line extends infinitely in both directions but a ray extends infinitely in one direction with a definite terminus in the other direction. In optics a ray extends infinitely in both directions so it is analogous to a geometrical line. In stigmatic imaging an object ray intersecting any specific point, A, in object space must be conjugate to an image ray intersecting the conjugate point A' in image space. A consequence is that every point on an object ray is necessarily conjugate to some point on the conjugate image ray.

Geometrical similarity implies the image is a scale model of the object. There is no restriction on the image's orientation. The image may be inverted or otherwise rotated with respect to the object.

Focal and afocal systems, focal points

In afocal systems an object ray parallel to the optical axis is conjugate to an image ray parallel to the optical axis. Such systems have no focal points (hence afocal) and also lack principal and nodal points. The system is focal if an object ray parallel to the axis is conjugate to an image ray that intersects the optical axis. The intersection of the image ray with the optical axis is the focal point in image space F'. Focal systems also have an axial object point F such that any ray intersecting is conjugate to a ray parallel to the optical axis. F is the object space focal point of the system.

Detailed explanations

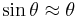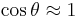The cardinal points lie on the optical axis of the optical system. Each point is defined by the effect the optical system has on rays that pass through that point, in the paraxial approximation. The paraxial approximation assumes that rays travel at shallow angles with respect to the optical axis, so that \sin\theta\approx\theta and \cos\theta\approx 1.[2] Aperture effects are ignored: rays that do not pass through the aperture stop of the system are not considered in the discussion below.

Focal planes

See also: Focus (optics) and Focal length

The front focal point of an optical system, by definition, has the property that any ray that passes through it will emerge from the system parallel to the optical axis. The rear (or back) focal point of the system has the reverse property: rays that enter the system parallel to the optical axis are focused such that they pass through the rear focal point.

The front and rear (or back) focal planes are defined as the planes, perpendicular to the optic axis, which pass through the front and rear focal points. An object infinitely far from the optical system forms an image at the rear focal plane. For objects a finite distance away, the image is formed at a different location, but rays that leave the object parallel to one another cross at the rear focal plane.

A diaphragm or "stop" at the rear focal plane can be used to filter rays by angle, since:

  1. It only allows rays to pass that are emitted at an angle (relative to the optical axis) that is sufficiently small. (An infinitely small aperture would only allow rays that are emitted along the optical axis to pass.)
  2. No matter where on the object the ray comes from, the ray will pass through the aperture as long as the angle at which it is emitted from the object is small enough.

Note that the aperture must be centered on the optical axis for this to work as indicated. Using a sufficiently small aperture in the focal plane will make the lens telecentric.

Similarly, the allowed range of angles on the output side of the lens can be filtered by putting an aperture at the front focal plane of the lens (or a lens group within the overall lens). This is important for DSLR cameras having CCD sensors. The pixels in these sensors are more sensitive to rays that hit them straight on than to those that strike at an angle. A lens that does not control the angle of incidence at the detector will produce pixel vignetting in the images.

Principal planes and points

The two principal planes have the property that a ray emerging from the lens appears to have crossed the rear principal plane at the same distance from the axis that that ray appeared to cross the front principal plane, as viewed from the front of the lens. This means that the lens can be treated as if all of the refraction happened at the principal planes. The principal planes are crucial in defining the optical properties of the system, since it is the distance of the object and image from the front and rear principal planes that determines the magnification of the system. The principal points are the points where the principal planes cross the optical axis.

If the medium surrounding the optical system has a refractive index of 1 (e.g., air or vacuum), then the distance from the principal planes to their corresponding focal points is just the focal length of the system. In the more general case, the distance to the foci is the focal length multiplied by the index of refraction of the medium.

For a thin lens in air, the principal planes both lie at the location of the lens. The point where they cross the optical axis is sometimes misleadingly called the optical centre of the lens. Note, however, that for a real lens the principal planes do not necessarily pass through the centre of the lens, and in general may not lie inside the lens at all.

Surface vertices

The surface vertices are the points where each surface crosses the optical axis. They are important primarily because they are the physically measurable parameters for the position of the optical elements, and so the positions of the other cardinal points must be known with respect to the vertices to describe the physical system.

In anatomy, the surface vertices of the eye's lens are called the anterior and posterior poles of the lens.[3]

Nodal points

The front and rear nodal points have the property that a ray aimed at one of them will be refracted by the lens such that it appears to have come from the other, and with the same angle with respect to the optical axis. The nodal points therefore do for angles what the principal planes do for transverse distance. If the medium on both sides of the optical system is the same (e.g., air), then the front and rear nodal points coincide with the front and rear principal points, respectively.

The nodal points are widely misunderstood in photography, where it is commonly asserted that the light rays "intersect" at "the nodal point", that the iris diaphragm of the lens is located there, and that this is the correct pivot point for panoramic photography, so as to avoid parallax error.[4][5][6] These claims generally arise from confusion about the optics of camera lenses, as well as confusion between the nodal points and the other cardinal points of the system. (A better choice of the point about which to pivot a camera for panoramic photography can be shown to be the centre of the system's entrance pupil.[4][5][6] On the other hand, swing-lens cameras with fixed film position rotate the lens about the rear nodal point to stabilize the image on the film.[6][7])

See also

Notes and references

  1. ^ Welford, W.T. (1986). Aberrations of Optical Systems. CRC. ISBN 9780852745648. 
  2. ^ Hecht, Eugene (2002). Optics (4th ed.). Addison Wesley. p. 155. ISBN 0-321-18878-0. 
  3. ^ Gray, Henry (1918). "Anatomy of the Human Body". p. 1019. http://www.bartleby.com/107/pages/page1019.html. Retrieved 12 Feb. 2009. 
  4. ^ a b Kerr, Douglas A. (2005). "The Proper Pivot Point for Panoramic Photography" (PDF). The Pumpkin. Archived from the original on 13 May 2006. http://web.archive.org/web/20060513074042/http://doug.kerr.home.att.net/pumpkin/Pivot_Point.pdf. Retrieved 05 Mar. 2006. 
  5. ^ a b van Walree, Paul. "Misconceptions in photographic optics". http://toothwalker.org/optics/misconceptions.html#m6. Retrieved 1 Jan. 2007.  Item #6.
  6. ^ a b c Littlefield, Rik (06 Feb. 2006) (pdf). Theory of the “No-Parallax” Point in Panorama Photography. ver. 1.0. http://www.janrik.net/PanoPostings/NoParallaxPoint/TheoryOfTheNoParallaxPoint.pdf. Retrieved 14 Jan. 2007. 
  7. ^ Searle, G.F.C. 1912 Revolving Table Method of Measuring Focal Lengths of Optical Systems in "Proceedings of the Optical Convention 1912" p.168-171.

External links